Square packing in a square

Square packing in a square is a packing problem where the objective is to determine how many squares of side 1 (unit squares) can be packed into a square of side a. Obviously, if a is an integer, the answer is a², but the precise, or even asymptotic, amount of wasted space for a a non-integer is an open question.

Proven minimum solutions:^[1]

Number of squares	Square size
1	1
2	2
3	2
4	2
5	2.707 (2 + 2^−1/2)
6	3
7	3
8	3
9	3
10	3.707 (3 + 2^−1/2)

Other results:

If you can pack n² − 2 unit squares in a square of side a, then a ≥ n.^[2]
The naive approach (side matches side) leaves wasted space of less than 2a + 1.^[1]
The wasted space is asymptotically o(a^7/11).^[3]
The wasted space is not asymptotically o(a^1/2).^[4]
11 unit squares cannot be packed in a square of side less than 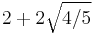$2%2B2\sqrt{4/5}$ .^[5]

References

^ ^a ^b Erich Friedman, "Packing unit squares in squares: a survey and new results", The Electronic Journal of Combinatorics DS7 (2005).
^ M. Kearney and P. Shiu, "Efficient packing of unit squares in a square", The Electronic Journal of Combinatorics 9:1 #R14 (2002).
^ P. Erdős and R. L. Graham, "On packing squares with equal squares", Journal of Combinatorial Theory, Series A 19 (1975), pp. 119–123.
^ K. F. Roth and R. C. Vaughan, "Inefficiency in packing squares with unit squares", Journal of Combinatorial Theory, Series A 24 (1978), pp. 170–186.
^ W. Stromquist, "Packing 10 or 11 unit squares in a square", The Electronic Journal of Combinatorics 10 #R8 (2003).